When is a Fresnel Lens not a Fresnel Lens?
It’s well known, to those who know it well, that diffractive optics and refractive optics suffer chromatic shift but that is opposite in sense. This is illustrated nicely by comparing a blazed grating with a Fresnel lens as shown below. Bear in mind these figures have more artistic license than a Pink Floyd album cover!
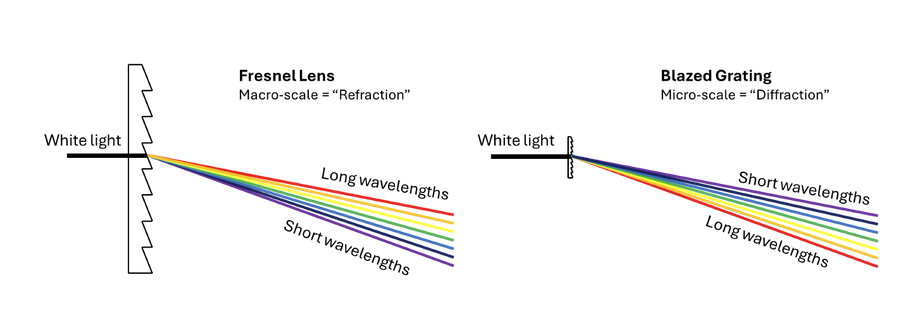
When we consider a beam of white light incident on a Fresnel lens, we usually refer to the light refracting through the inclined surface of the macroscopically sized “teeth”. That is, teeth on a millimeter scale or so. What we find is that the white light spreads into a spectrum with shorter wavelengths (blue, violet, ultra-violet) refracting more than the longer wavelength (red, infra-red).
When the teeth are micro-scale (on the order of wavelengths) we refer to a blazed grating diffracting light. What we find in this case is that longer wavelengths deviate more than shorter wavelengths, the opposite of the macro case.
That begs the question, what happens between these two extremes? Is there an intermediate scale which is achromatic where all wavelengths deviate with the same angle?
Let’s go back to basics for a moment.
When light of wavelength (λ) is incident on a simple diffraction grating (thin slits a distance d apart), it diffracts into various orders, m, where the positive and negative orders are symmetrical.
We are probably all familiar with the diffraction equation which tells us the angles of diffraction (ϴ):
mλ=d sinϴ
The diffraction angles, of course, occur when the light from neighbouring slits are in phase (integer wavelengths apart) and constructively interfere as described below.
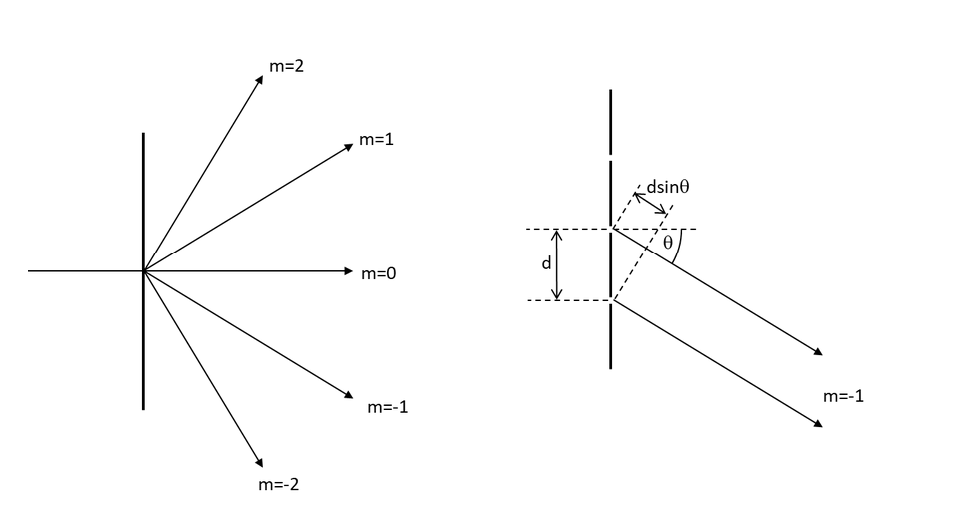
If the slits are widened, we still have constructive interference between slits but not within a slit. In the figure below, rays A and C are in phase, but rays A and B are not. Path lengths from points within a slit cannot all be integer wavelengths apart. However, if the slits are replaced by small prisms with an appropriate wedge angle (Ɛ) all light emerging from any prism can be in phase and of course will constructively interfere with light emerging from other prisms. This only works for one order at one wavelength and is the principle of a blazed grating. What may not be obvious is that the angle, Ɛ, is the same angle as you would require using Snell’s Law to refract in the same direction.
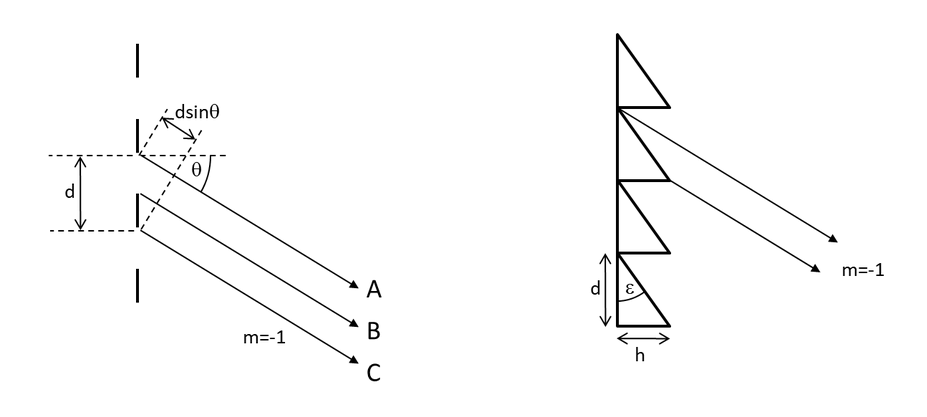
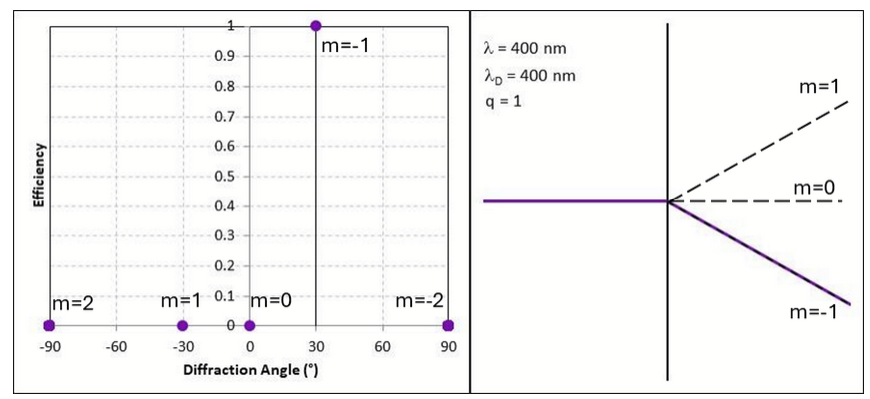
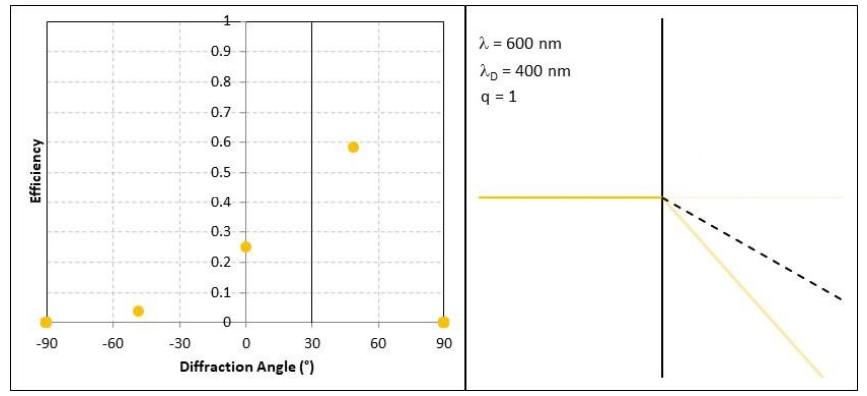
Let’s look at an example. Consider a blazed grating designed to deflect light of 400nm (λD) wavelength 30° using first order (q=1) diffraction. Here q is the design order of diffraction at a particular wavelength, m is the resulting order (or orders) of diffraction we see. Without going into the mathematics, this is achieved with a prism width, d, of 0.8µm and a prism angle of 23.5°. The height, h, of the prism is 0.35µm. The prism angle depends on the material refractive index which in this case is about 1.9. A very dispersive material (N-SF66) was used to exaggerate the refractive dispersion.
Below is the result of a simulation of this diffraction with incident light at 400nm. All the light diffracts into the m=-1 order at 30° (because it’s designed that way). Other orders exist but have zero efficiency. The right-hand plot shows a simulated ray trace which shows diffraction into the m=-1 direction.
What happens as we change the wavelength? At 600nm for example two things happen. First order diffraction increases in angle to 48° and the m=-1 efficiency drops as light leaks into the m=0 and m=1 orders. We can just see the zero-order ray emerging in the ray trace plot.
To illustrate this better, the GIF below shows an animated wavelength scan from 400-800nm. Notice the plots change color to match the wavelength, turning black at infra-red wavelengths.
Let’s now gradually transition the blazed grating to a macro scale. First, make the prisms twice as large. They are still the same angle, but d becomes 1.6µm and h becomes 0.7µm. What this means is that diffraction designed for 400nm is now second order diffraction (q=2). So, m=-2 is 100% efficient at 30°. First order diffraction is now zero efficiency at 400nm.
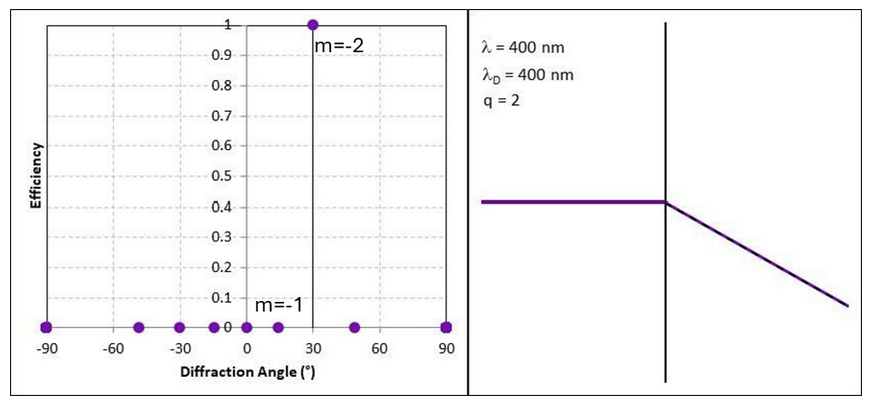
The animation of this (below) shows all the diffraction orders (except zero) increase the diffraction angle as wavelength increases and that at 800nm we see first order diffraction at exactly 30°. So the 2nd order at 400nm and 1st order at 800nm diffract at the same angle. You also notice that the 800nm efficiency is not quite 100%. This is because the refractive index at 800nm is not ideal. Also, the peak efficiency is at a wavelength lower than 800nm. What this does show is that a lens made to this specification would be achromatic at these two discrete wavelengths, but not between.
Let’s see what happens at 5 times as large (d=4µm). We are starting to see that the profile of efficiency variation becomes narrower with most of the orders have virtually zero efficiency. There are multiple wavelength and multiple orders which diffract at 30°. This type of diffraction is referred to as multi-order diffraction (MOD).
At 10 times as large (d=8µm) the profile of efficiency variation is narrower still and we start to see that although the diffraction orders increase in angle with wavelength the peak efficiency wavelength shifts to lower angles. The 5th order of 800nm is still diffracting at 30° but is less than 30% efficient.
At q=50 (d=40µm) virtually all orders have close to zero efficiency and so we only see the high efficiency rays. These shift to lower angles with increasing wavelength.
Now let’s jump to q=1000 (d=0.8mm). We are now very much macroscopic, and we would describe this as a Fresnel lens refracting light even though this is diffraction modeling. The modeling is limited to +/-1000 orders so we don’t see the orders higher than that in this simulation.
So, when is a Fresnel lens not a Fresnel lens? When it’s a very high order MOD lens!
And, no, we don’t find a magical achromatic zone of “micro-Fresnel” optics, but then if it existed, we’d already know about it, wouldn’t we? However, if we have applications where we are only interested in a few discrete wavelengths (e.g. 1064nm and 532nm) we can design a multi-order diffractive lens that can be achromatic, and Selene Development can provide diamond turned prototypes and molded production optics.
In summary, the diffraction angle always increases with wavelength. The angle that reduces with wavelength is the peak efficiency angle and as we transition from diffraction to refraction we only observe those diffraction orders close to peak efficiency. Other orders fall quickly to zero efficiency.
